GEOGEBRA

¿Qué es GeoGebra?

GeoGebra es un software matemático interactivo libre para la educación en colegios y universidades. Su creador Markus Hohenwarter, comenzó el proyecto en el año 2001 en la Universidad de Salzburgo, lo continuó en la Universidad de Atlantic, Florida, luego en la Universidad Estatal de Florida y en la actualidad, en la Universidad de Linz, Austria.

Es básicamente un procesador geométrico y un procesador algebraico, es decir, un compendio de matemática con software interactivo que reúne geometría, álgebra y cálculo.

¿Para qué sirve?

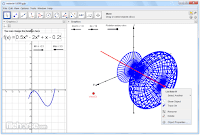GeoGebra permite el trazado dinámico de construcciones geométricas de todo tipo así como la representación gráfica, el tratamiento algebraico y el cálculo de funciones reales de variable real, sus derivadas, integrales, etc.

Puede ser usado en física, proyecciones comerciales, estimaciones de decisión estratégica y otras disciplinas.

¿Cómo lo puedo obtener?

Desde la página https://www.geogebra.org/download aparecen las distintas opciones para descargar la aplicación. 

También puede obtenerse a partir de páginas externas, pero lo más recomendable es descargarlo desde la página oficial o desde la tienda de aplicaciones del propio sistema operativo.

GeoGebra está escrito en Java y por tanto está disponible en múltiples plataformas:

• Windows: todas.
• macOS: 10.6 en adelante.
• Linux: compatible con Debian, Ubuntu, Red Hat y OpenSUSE.
• Android: depende del dispositivo.
• iOS: 6.0 o posterior.

¿Cómo se usa? (Manual)

Contenido
1 Gráficos de Funciones a Deslizar Dinámicamente
2 Parámetros y su función en las Funciones
2.1 Preparativos
2.2 Registro Gráfico en correlato con los Parámetros de la Expresión
2.2.1 Paso a Paso
2.3 Graficando Funciones
2.3.1 Usando Deslizadores
2.3.2 Cajas de Diálogo
3 Repertorio de Funciones
3.1 Preparativos de Valor Absoluto
4 Desafío Periódico
5 Introducción a Derivadas – La Pendiente
5.1 Preparativos
5.2 Pasos de Construcción
6 Exploración y Desafños...
7 Explorando Polinomios
7.1 Preparativos
7.2 Pasos de Construcción
8 Exportando una Imagen al Portapapeles
9 Exportando Gráficos al Portapapeles
9.1 Crear o Seleccionar el Boceto
9.2 Exportando Gráficos al Portapapeles
10 Intercalando la Gráfica en un Documento
10.1 Intercalando gráficos desde el pontapapeles a un documento de texto
10.2 Acotar las medidas del contenido gráfico pegado
10.3 Pegar y desde el Portapapeles en otros Procesadores de Texto
10.4 Reducción de medidas en otros procesadores de texto

Gráficos de Funciones a Deslizar Dinámicamente

GeoGebra permite trazar las gráficas de una variedad de funciones - como ilustra la figura - y de calcular las áreas bajo las curva.

Parámetros y su función en las Funciones

En este tutorial, se va a indagar sobre el efecto de los parámetros de diversas funciones, empleando los deslizadores de GeoGebra para modificarlos y registrar correlatos en las representaciones gráfica.

Preparativos

En el Menú Apariencias, es preciso seleccionar la adecuada y:

• dejar activa la Barra de Estilo
• exponer los ejes de coordenadas.

Reconocer las herramientas que van a emplearse:

	Deslizador
	Recta: y = m x + b
	Segmento
	Interseca[recta, EjeY]
	Intersección
	Pendiente
	Objeto (in)visible
	Elige y Mueve

Registro Gráfico en correlato con los Parámetros de la Expresión

En primer lugar, se indagará qué cambios se registran sobre la función "y = mx" - empezando por anotarla en la Barra de Entrada - y emplear los deslizadores para modificarla.

Paso a Paso

Para seguir este tutorial paso a paso, se puede abrir la Ventana de GeoGebra en el buscador. La salidas de una versión se pueden observar aquí .

Incluso se puede recurrir al artículo que, en inglés, permite controlar los deslizadores, en cuatro pasos (Graphs and Sliders Part 2.)

Graficando Funciones

1. Abrir GeoGebra para graficar y = 2x simplemente anotando y = 2x en la Barra de Entrada y pulsando Intro (ENTER en algunos teclados)
2. Anotar las siguientes ecuaciones: y = 3x así como y = 4x y finalmente y = -8x pulsando la tecla Intro tras cada una de ellas.
3. Se pueden ensayar otras ecuaciones de formulación y = m x dándole a m cualquier valor real.
4. ¿Cómo impacta sobre el gráfico cada cambio en el valor de m ?

Usando Deslizadores

Para evitar tener que anotar una y otra vez el valor diferente que se quiera ensayar para el parámetro - m en este caso y el de que se tratara en general -, se puede emplear como sintonizador de control de valores un deslizador .

Un deslizador es la 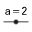 representación visual de un número que en esta ocasión emplearemos no solo para m sino también para b. Lo que implica que se podrá explorar en gráfico de la función y = mx + b dándole a m y a b diferentes valores reales.

Cajas de Diálogo

Se pueden registrar los efectos de estos pasos:

• 1.) Abrir la Ventana de Geogebra
• 2.) Seleccionar la 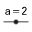 Herramienta de Deslizador, dar un clic en cualquier lugar libre de la Vista Gráfica para abrir la Caja de Diálogo correspondiente.

• 3.) En la Caja de Diálogo , cambiar:
  • el nombre del deslizador por m,
  • el intervalo - en la pestaña correspondiente - para que se extienda entre un Mín - mínimo - de -10 y un Máx - máximo - de 10 .
  • si se lo desea, el incremento a, por ejemplo, 0.25 , manteniendo los demás valores sin modificaciones y dejando todo establecido al pulsar el botón Aplica para aceptarlos y salir.

Nota: En la Caja de Diálogo del deslizador, en cada una de las pestañas, es posible además:

• Establecer...
  • su disposición Horizontal o Vertical y
  • el Ancho que presentará
• Asignarle una Animación que afectará a todo lo que dependa del deslizador...
  • con una modalidad (Oscilando, Incrementando... ) y
  • Velocidad acorde a lo que se indique.

4. ) En la Vista Gráfica, ajustar la posición del deslizador (y el color) de ser necesario y luego, mover el redondelito que opera como sintonizador para registrar los efectos que se operan.

5.) Llevar adelante las mismas maniobras para el deslizador b (eligiendo un color contrastante y diferente del que se eligió para m ).

6.) Anotar ahora en la Barra de Entrada, la expresión m x + b reemplazando la última ingresada (en este ejemplo, 3 x ) para observar ahora qué sucede cuando se cambia la sinfonía - y por lo tanto, el valor - para cada deslizador vinculado a esta expresión y a su gráfico.

7.) Marcar:

• el punto de intersección entre la lineal y el EjeY
• el  segmento entre el origen de coordenadas y el punto de intersección recientemente creado con el mismo color que se le hubiera asignado a b .
•  un punto sobre la gráfica lineal y emplear la  Herramienta de Pendiente para poner en evidencia el impacto del deslizador correspondiente.

Nota: Anticipar lo que se supone sucedería si se le diera animación al deslizador correspondiente a:

• m
• b

... y controlar, realizando la maniobra, si efectivamente se confirma tal presunción.

 Pista: La animación sobre un deslizador puede desactivarse simplemente seleccionándolo con un clic derecho para quitar el tilde en la opción correspondiente del Menú Contextual que se despliega. Esta maniobra no es posible cuando se detiene momentáneamente la animación con el botón pertinente.

A tener en cuenta...

 Pista: El símbolo ^ se emplea para anteponer e indicar un exponente en GeoGebra. Por eso, para hacer ensayos con otros deslizadores - n , a , b y c por ejemplo - y otras funciones - a x^n + b x + c es necesario identificar:

• dónde se encuentra el símbolo correspondiente a ^
• en su defecto, ingresar, cuando se trate de un cuadrado o un cubo, el superíndice que ofrece la caja de símbolos básicas que se despliega pulsando la flecha a la derecha de la Barra de Entrada

Repertorio de Funciones

Más allá de los polinomios que pueden ingresarse directamente en la Barra de Entrada, es posible apelar a cualquier de los diferentes tipos de funciones disponibles en GeoGebra (sean las trigonométricas, las exponenciales, las de valor absoluto, módulo o resto...). Con las funciones se puede operar como con cualquier otro objeto e incluso combinarse con construcciones geométricas o con datos que se registren en las celdas de una Hoja de Cálculo.
Nota: Se puede incluso operar con funciones de funciones para modelizar, por ejemplo, cuestiones como la que aparece en una sinusoidal portadora de una función que modula tanto su amplitud como su frecuencia.

Preparativos de Valor Absoluto

1 Abrir una nueva ventana de GeoGebra y seleccionar del Menú Apariencias una que incluya la Vista Algebraica, Barra de Entrada y ejes de coordenadas.
2 Preparar un deslizador a, inicialmente con el valor 3...
• para afectar a la función constante a anotar g(x) = a e
• ingresar una versión, libre y por tanto desplazable con las teclas de flecha - abs(x) -.
3 Buscar la intersección entre una y otra función.

1	f(x) = abs(x)	Se ingresa la función de valor absoluto para explorar su comportamiento.
2	y = 3	Se ingresa la función constante, que aparece con el nombre 'g en el gráfico para indagar todo lo posible, al ir desplazándola, respecto de las relaciones que vinculan a los puntos de intersección con abs(x).
3		Se trazan los puntos de intersección entre la función abs(x) y la constante paralela al EjeX  Pista: Es preciso aplicar dos veces, una en cada rama de la función abs(x), la herramienta de intersección para obtener sendos puntos.

 Pista: Se puede decidir el cierre de la Vista Algebraica en tanto se dispongan los rótulos con nombres y valores de los objetos con los que se opera.

Desafío Periódico

Las ondas de sonido pueden ser matemáticamente representadas como una combinación de sinusoide. Cada nota musical está compuesta de varia sinusoides de formulación y(t) = a sin(ω t + φ) . La amplitud aafecta el volumen y la frecuencia angular ω determina el timbre. El parámetro φ se denomina fase porque la indica en la onda de sonido.
Si dos sinusoides se superponen, interfieren entre sí de modo tal que una amplifica o reduce la amplitud de la otra. Es posible representar este modelo de estudio del fenómeno para examinar casos especiales.

1	Deslizador	Crear tres deslizadores a_1, ω_1, y φ_1  Pista: El guion bajo entre la a y el 1 lo determina como subíndice. Las letras griegas se pueden seleccionar del menú próximo al campo de texto en la ventana de diálogo del deslizador.
2	g(x)= a_1 sin(ω_1 x + φ_1)	Ingresar a continuación la función seno g  Pista: Nuevamente, se pueden seleccionar las letras griegas del menú junto a la Barra de Entrada

(a) Examinar el impacto de los parámetros - cambio de los valores de los deslizadores - sobre el gráfico de las funciones sinusoidales.

3	Deslizador	Crear tres deslizadores a_2, ω_2, y φ_2  Pista: Los deslizadores solo se pueden mover cuando la correspondiente herramienta es activada.
4	h(x)= a_2 sin(ω_2 x + φ_2)	Ingresar la otra función seno - h -
5	sum(x) = g(x) + h(x)	Anotar la suma de ambas funciones en la Barra de Entrada

(b) Cambiar el color de las tres funciones para distinguirlas con más facilidad.
(c) Fijar a_1 = 1, ω_1 = 1, y φ_1 = 0.
(d) Operar sobre los deslizadores para dar respuesta a los siguientes interrogantes:
• ¿Para qué valores de a_2, ω_2, y φ_2 la suma tiene amplitud máxima?
   Pista: En este caso el tono resultante tendrá volumen máximo.
• ¿Para cuáles las dos funciones se cancelan mutuamente?
   Pista: En este caso, el tono dejará de ser audible.



Introducción a Derivadas – La Pendiente

Dado que en esta propuesta van a emplearse la serie de herramientas que se listan a continuación y comandos desde la Barra de Entrada, conviene familiarizarse con su empleo antes de comenzar.

	f(x) = x^2/2 + 1
	Punto
	Tangentes
	Con la herramienta o el comando, se calcula la Pendiente de t
	S = (x(A), slope)
	Segmento
	Elige y Mueve

Preparativos

1 Abrir una Nueva Ventana de GeoGebra.
2 Seleccionar la de Álgebra y Gráficos en el Menú Apariencias

Pasos de Construcción

1. Anotar en la Barra de Entrada el polinomio: f(x) = x^2/2 + 1
2. Crear un nuevo punto A sobre la función f.
 Pista: Para comprobar que está restringido a la gráfica de la función, basta con desplazar A.
3. Trazar la tangente t a la función f en el punto A.
4. Establecer la pendiente de la tangente t anotando, en la Barra de Entrada: pendient_e= Pendiente[t]
5. Establecer el punto de definición algebraica S, en la Barra de Entrada, como S: S = (x(A), pendient_e)
 Pista: x(A) brinda la abscisa del punto A.
6. Trazar un segmento entre los puntos A y S.

Exploración y Desafños...

Se puede...
• Pedir una anticipación sobre el tipo de rastro que va a dejar el punto S al desplazar A a lo largo de la gráfica de la función f y preguntarse a qué corresponde ese trazo.
• Corroborar si lo que se presupuso fue correcto, dando rastro a S y desplazando A.
   Pista: Un clic derecho sobre S (MacOS: Ctrl + clic) permite activar el Rastro en el Menú Contextual desplegado.
• Intentar una ecuación a ingresar en la Barra de Entrada para verificar si su gráfica coincide con el rastro de S.
• Cambiar los datos, coeficientes y la ecuación polinomial original para plantearse y resolver nuevos problemas.

Explorando Polinomios

Preparativos

1 Abrir una Nueva Ventana de GeoGebra.
2 Seleccionar la de Álgebra y Gráficos en el Menú Apariencias

Pasos de Construcción

1	f(x) = 0.5x³ + 2x² + 0.2x - 1	Ingresar en la Barra de Entrada la polinomial cúbica f
2	R = Raíz[ f ]	Establecer las raíces del polinomio f  Pista: Si hubiera más de una, GeoGebra establecerá sub-índices para sus nombres. Por ejemplo, para R --- R1, R2, R3).
3	E = Extremo[ f ]	Establecer los extremos del polinomio f (llamados también Puntos de Inflexión y/o Puntos Notables)
4		Establecer los tangentes del polinomio f' en E1 y E2
5	I = PuntoInflexión[ f ]	Establecer los puntos de inflexión del polinomio f'

 Pista: Conviene cambiar las propiedades de los objetos para que sea adecuado el contraste de colores, el estilo de las tangentes y que queden expuestos nombres y valores, como los de la función).



Exportando una Imagen al Portapapeles

Cada Vista Gráfica de GeoGebra se puede exportar, completa, al portapapeles del sistema para incluir bocetos ilustrativos en diversos documentos, sean de presentaciones o de texto - pruebas, exámenes, notas, desafíos o guías de trabajos prácticos -.

Exportando Gráficos al Portapapeles

Crear o Seleccionar el Boceto

Abrir la ventana de GeoGebra para corroborar que esté abierta la Vista Algebraica y, de ser necesarias la Barra de Entrada, la cuadrícula y los ejes de coordenadas. Si en lugar de seleccionar de entre las propuestas de la wiki o del repertorio de recursos que se brinda en alguno de los Talleres ofrecido a los docentes, se prefiere preparar el boceto del que ir copiando sucesivas ilustraciones al portapapeles para pegarlas en un documento en marcha, es aconsejable mantener sendas ventanas abiertas - la del procesador y la de GeoGebra - y, en particular, tener armado un boceto dinámicamente dúctil. Por ejemplo...

1	n=1 c=x(C)	Preparar un deslizador - n - que establezca el grado de la función con la que se va a operar y marcar dos puntos sobre el eje de abscisas que determinarán el valor inicial y el de terminación que limitarán el rango de la variable independiente en las operaciones.
2	an = 3 a1 = 0.2 ao= -1	Plantear deslizadores para cada uno de los coeficientes de la función con la que eventualmente se e va a operar.
3	a3 x³ + a2 x² + a1 x + ao	Ingresar los diversos polinomios que se podrán seleccionar según el grado n en que se decida operar. Por ejemplo, el cúbico f que depende de los tres coeficientes previamente establecidos.
4	Raíz[ f ]	Indicar las raíces del polinomio que se hubiera seleccionado, estableciendo la coordenada x correspondiente a cada punto  Pista: Si hubiera más de una raíz GeoGebra las distinguirá colocando el índice correspondiente a sus nombres como, por ejemplo, R1, R2, R3).
5	Extremo[f]	Establecer los extremos del polinomio f en juego.
6		Trazar tangentes de f en cada punto extremo (como E1 y E2, por ejemplo).
7	PuntoInflexión	Marcar el punto de inflexión del polinomio seleccionado PuntoInflexión[f ] .

 Pista: Puede ser conveniente modificar las propiedades de los objetos (como el color de los puntos o el estilo de una recta que cumpla determinado rol, exponer o no el nombre y formulación de la función o establecer que ciertos valores se expongan como fracciones, antes de exportar).

Exportando Gráficos al Portapapeles

Es conveniente reducir la Vista Gráfica antes de copiarla al portapapeles para evitarse el espacio innecesario. Se la puede acotar con maniobras simples:
• Desplazar la imagen (o la sección más relevante) a la esquina superior izquierda de la Vista Gráfica empleando la herramienta que la desplaza (como se ilustra a continuación).
   Pista: Se puede completar esta operación empleando las herramientas de Aproximar y de Alejar para encuadrar mejor lo que se va a exportar.
• Reducir la medida de la ventana de GeoGebra arrastrando su esquina inferior derecha con el ratón o mouse.
   Pista: El puntero cambia de forma cuando pasa por encima de los bordes o de las esquinas de la ventana de GeoGebra.
Emplear el Menú Archivo para exportar la Vista Gráfica al portapapeles:
• Exporta – Vista Gráfica al Portapapeles
   Pista: También se puede emplear la combinación de teclas Ctrl + Shift + C
.
• El contenido de la Vista Gráfica está efectivamente almacenado en el portapapeles del sistema y se puede pegar en cualquier documento que se estuviera editando.

Intercalando la Gráfica en un Documento

Después de exportar el contenido de la Vista Gráfica de GeoGebra al portapapeles del sistema, se lo puede pegar en cualquier documento que se estuviera preparando con un procesador de textos.

Intercalando gráficos desde el pontapapeles a un documento de texto

• Abrir el documento que se estuviera procesando
• Ubicar el cursor en la posición en que se quiere pegar el gráfico y acudir a la opción del menú que realice la operación deseada o apelar a la combinación de teclas correspondiente - generalmente, Ctrl + V -

Acotar las medidas del contenido gráfico pegado

Para recudir las medidas de lo intercalado en el documento, si fuera necesario, en general, basta con...
• un doble clic sobre la imagen
• cambiar las medidas de la altura y el ancho en la caja de diálogo emergente que usualmente tiene una opción de medidas para el grupo asociado al gráfico..
Nota: De cambiar la medida de la imagen, la escala se modifica también. Para mantener la escala (lo que puede ser importante si parte del desafío incluido en el documento implica medicines de longitud, por ejemplo), es preciso asegurarse de conservar el gráfico al 100%.
Nota: Si el gráfico es demasiado amplio para entrar en una página del documento, muchos procesadores automáticamente lo reducen con el consiguiente cambio de escala.

Pegar y desde el Portapapeles en otros Procesadores de Texto

• Abrir el documento
• Proceder a pegar desde el menú o con la correspondiente combinación de teclas Ctrl + V.

Reducción de medidas en otros procesadores de texto

Suelen funcionar maniobras similares a las descriptas y, en todo caso, la ayuda del procesador en juego orientará en el procedimiento.